Continuous time or event time models have a long history in human biomedical sciences. In wildlife ecology, event-time analyses are often applied to studies where time to failure or time to death is known. These models are used with increasing frequency as high resolution location data have become common, particularly for large species including cervids.

A typical study design involves capturing and marking a random sample of individuals from a population of interest. Marked individuals are then recaptured at a later time, or re-sighted at an interval throughout the length of the study. The status of these marked individuals at these fixed interval times, i.e. alive or dead, are used to estimate the probability of survival. The time to death in survival is the random variable in these studies.

The construction of event time models can allow for both interval and right censoring, as well as staggered entry or left truncation of individuals. The foundation of this model is the hazard function, which can take any mathematical form. Common choices include a constant hazard, log-logistic, Weibull, piece-wise constant, and intrinsic conditional auto-regressive models.

The likelihood for these data follow the form (Heisey et, 2007; Walsh et al, 2017):

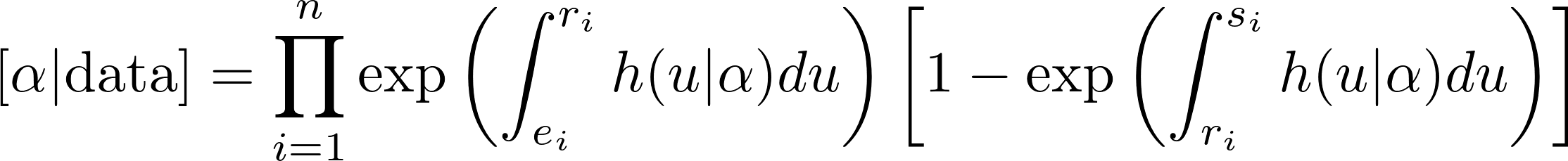
for i=1,…,n marked individuals. Parameters include:

The time scale for the interval during which an individual may have died can be chosen based on data availability and species specific life histories (i.e. months, weeks, days, hours).